I matematik lærer du at tænke logisk og abstrakt, at analysere og løse problemer, og du får redskaber til bedre at forstå verden omkring dig. Grundlæggende arbejder vi med at undersøge, beskrive og forstå forskellige strukturer. Disse strukturer er ofte knyttet til den verden vi lever i, fx fysikkens verden, men også menneskeskabte systemer som valg og økonomi.
Geometri
Geometri hører til de ældste discipliner inden for matematikken. I oldtidens Egypten brugte man geometri til at opmåle marker for at kunne beregne de skatter, som bønderne skulle betale. Op igennem historien kan flere af de store landvindinger inden for geometrien knyttes til konkrete behov for at kunne opmåle verden.
I matematik arbejder vi med trigonometri, som er den geometri, der vedrører trekanter. Hertil lærer og beviser vi en række trigonometriske formler.
For at se hvordan trigonometri kan bruges i praksis, arbejder vi med et projekt om landmåling og opmålingsmetoden triangulering. Triangulering betyder, at man deler landskabet ind i en lang række trekanter. Trekanternes hjørner er synlige lokaliteter i landskabet som kirker eller bakker. Hvis man måler samtlige vinkler, er det kun nødvendigt at måle en enkelt side, basislinjen. Ved passende trigonometriske formler er det nu muligt at beregne samtlige sider. På den måde gør matematikken det muligt at lave præcise kort uden at skulle måle afstandene, hvilket er meget vanskeligt og tidskrævende.
Vækst
Arbejdet i de naturvidenskabelige fag tager ofte udgangspunkt i et eksperiment. Ved eksperimentet måles typisk en række sammenhørende værdier af to varierende fysiske størrelser. Man står nu med det rent matematiske problem at skulle afgøre, hvilken sammenhæng der er tale om.
Et godt eksempel er den såkaldte håndtryksøvelse. Øvelsen går ud på, at man måler den tid, som det tager et signal at nå gennem en kæde af elever, som holder hinanden i hånden. Signalet bevæger sig ved, at eleverne - når de mærker et klem i den ene hånd - klemmer den elev, som de holder i den anden hånd. Det er klart, at den tid det tager at nå igennem kæden afhænger af, hvor mange personer der er i kæden. Hvis man måler sammenhørende værdier for antal personer og tid, så får man en graf, som kunne se ud på følgende måde:
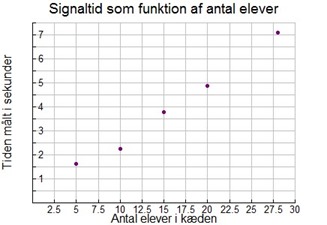
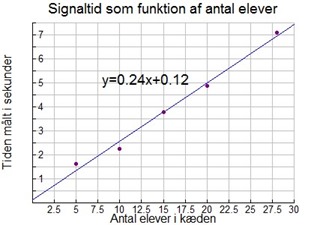
På figur 2. ses den bedste rette linje indtegnet, og med regression har man bestemt forskriften. Den fortæller blandt andet, at signalet er 0,24 sekunder om at nå igennem én person. Funktionsforskriften giver også mulighed for at komme med konkrete forudsigelser: Hvor lang tid det vil tage signalet at nå igennem en lang kæde af alle eleverne på skolen?
Sandsynlighedsregning og statistik
Man kan ikke åbne en avis eller se nyheder uden at støde på resultater af statistiske undersøgelser. Få statistiske resultater kan give os et hurtigt overblik over forskellige samfundsmæssige forhold som ellers var uoverskuelige. Således har statistik og sandsynlighedsteori en stor indflydelse på vores meningsdannelse og på den offentlige debat.
I statistik kan man arbejde med om givet datasæt er udtryk for en bestemt tendens. Det forgår ved at lave forskellige typer tests på datamaterialet.
Konkret kan man undersøge: Er der sammenhæng mellem, hvilken studieretning man har valgt, og hvor i det politiske spektrum man stemmer? For at kunne besvare spørgsmålet, er man nødt til at uddele spørgeskemaer, sammentælle og bruge relevant statistisk test til at afgøre om der er sammenhæng.
Et andet eksempel er behandling af meningsmålinger i forbindelse med folketingsvalg eller kommunalvalg. Hvem vinder valget? Hvor sikre er vi på resultatet?